
Mathematics is a pure and beautiful discipline. Much of it is arcane and theoretical, way beyond the grasp of the average person, but you would be surprized to discover how many things in everyday life came about because of the application of mathematics.
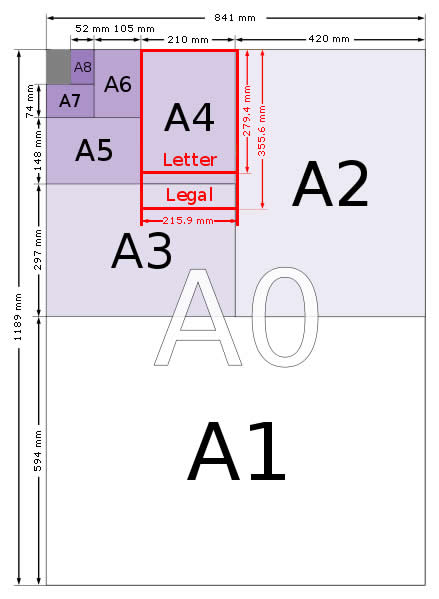
For example, take the standard A4 sheet of paper. Do you think it was haphazard or random that the dimensions 297 millimetres by 210 millimetres were chosen? Was it simply good luck that these exact dimensions have the property that by folding a piece of paper this size in half you get another sheet that is smaller but proportionally identical (meaning that the ratio of the long side to the short side is the same)? And if you put two A4 sheets next to each other the size is again proportionally identical. Was that a coincidence, or what?
Certainly not. The simple but incredibly useful property that any A4 sheet of paper can be doubled or halved in size, successively and infinitely, and in each case the ratio of the length of the long side to that of the short side remains constant is the result of some simple mathematics. The actual lengths of the two sides don't matter - it is the ratio of the lengths that counts.
Here's the problem : What ratio of short side length to long side length do you need to ensure that doubling or halving the page retains the ratio?
| Let's set the short side length to 1. |
| We don't know what the long side length should be so we'll call that "x". |
| Thus the ratio we need to keep constant is 1:x or 1/x. |
| If you cut the paper in half then the short side (length 1) becomes the long side, and the existing long side (length x) is halved. So the ratio of our new smaller page, short side to long is x/2 : 1 or simply x/2. |
| But for the ratio to remain constant after halving the page it means that |
| 1/x = x/2 |
| 1 = x2/2 |
| x2 = 2 |
x = 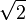 |
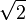 bigger (meaning that you multiply the short side length by
bigger (meaning that you multiply the short side length by 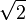 to get the long side length). Thus, a standard A4 sheet has a short side length of 210 millimetres, so the long side length is 210
to get the long side length). Thus, a standard A4 sheet has a short side length of 210 millimetres, so the long side length is 210 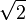 = 296.985 millimetres.
= 296.985 millimetres.
But again you may ask, why 210 mm? Why not 250 mm? Or 175 mm? To see how the A4 size was derived, look at the picture on the right, which shows the size of the "base" (A0) page as 1189 millimetres by 841 millimetres. How were these odd numbers chosen? Again, very simply - it was decided to base all standard pages on an initial page of one square metre in area. So what are the dimensions of a page that is one square metre in size but which uses the 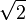 ratio as described above? Applying similar logic to that we used before:
ratio as described above? Applying similar logic to that we used before:
| Let's say the long side length is "x" and the short side length is "y". |
| The area of the base page must be one square metre, so xy = 1. |
But the ratio x/y = 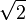 . . |
So y = x / 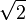 |
| And y = 1 / x |
Therefore 1 / x = x / 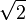 |
x = 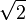 / x / x |
x2 = 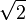 (which means x is the square root of (the square root of 2)) (which means x is the square root of (the square root of 2)) |
| x = 1.189207 metres = 1189.207 millimetres |
So y (the short side length) must be 1189.207 / 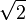 |
| y = 840.897 millimetres |
Once the exact size of the A0 page was determined, the size of each smaller page (A1, A2, A3, ...) followed automatically from that. Simple and elegant.
 © Paul Kilfoil, Cape Town, South Africa
© Paul Kilfoil, Cape Town, South Africa